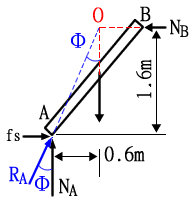
取AB桿為自由體如圖所示，W、R_A、N_B三力平衡必相交於一點 O

μ = tan Φ = 0.6/1.6 = 3/8 =0.375

另外解法

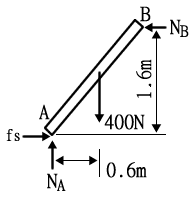
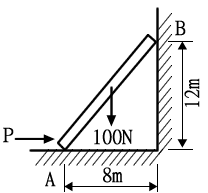
N_A=400(N)

ΣM_A=0

N_B×1.6-400×0.6 = 0

N_B = 150(N)

f_s = μ×N_A = N_B

μ×400 = 150

μ = 150 / 400 = 0.375

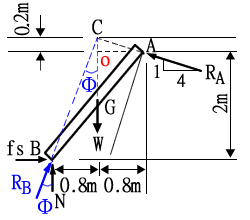
OA=0.8m → OC=0.2m

取AB桿為自由體如下圖所示 當W、R_A、R_B（f_S與N之合力）三力平衡時，必相交於一點C，所以由幾何關係知：

μ＝tanΦ＝0.8/(2+0.2)＝0.36

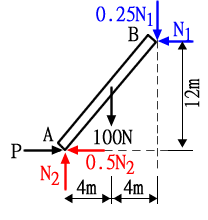
ΣM_A=0 → 100×4＋0.25N₁×8－N₁×12＝0

N₁＝400/10 ＝40(N)

ΣF_y＝0 → N₂－100－0.25×40＝0

N₂＝110(N)

ΣF_x＝0 →P－0.5×110－40＝0

P＝95(N)

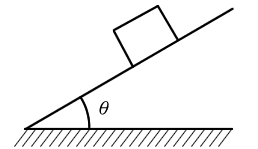
摩擦角=30°

故摩擦係數 μ=tan30°=√3/3

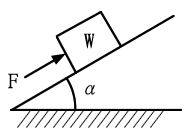
物體A的重量 W 與斜面垂直的分力=Wcosα

物體A的重量 W 與斜面平行的分力=Wsinα (往下滑的力量)

摩擦力=μWcosα

因為有摩擦力，所以只要出力 F = Wsinα - μWcosα=W(sinα - μcosα)

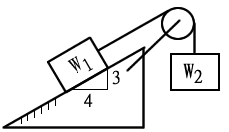
物體A的重量 500N 與斜面垂直的分力=500×4/5=400N

物體A的重量 500N 與斜面平行的分力=500×3/5=300N (往下滑的力量)

摩擦力=0.4×400=160N

因為有摩擦力，W₂之最大值（物體往上運動）＝300＋160＝460N

因為有摩擦力，W₂之最小值（物體往下運動）＝300－160＝140N

比460N大，物體往上運動，比 140N 小 物體往下運動，因此選 120N

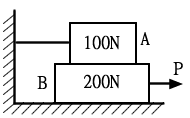
A 與 B 之間的摩擦力=100×0.2=20N

B 與地面之間的摩擦力=(100＋200)×0.2=60N

P=20+60=80N

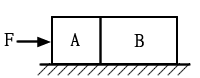
A物體10×9.8=98N

摩擦力=98×0.5=49N

B物體20×9.8=196N

摩擦力=196×0.25=49N

所以F=49＋49=98N