A 20N
B 50N
C 70N
D 90N
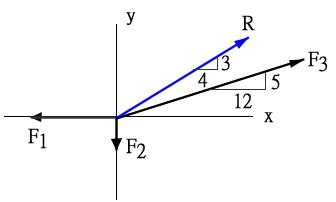
如圖所示
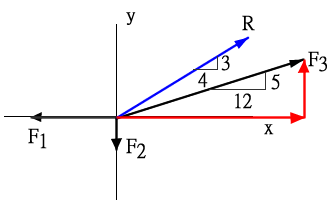
`vec(F_3)`可以分解成 `vec(水平)` 跟 `vec(垂直)` 分量(紅色)
因為 `vec(F_3)` 是 5,12,13三角形
`vec(水平)` = 130*12/13 = 120N,垂直分量 = 130*5/13 = 50N(用不到)
`vec(水平)` 跟`vec(F_1)` 分向相反,所以抵消,剩下120 – 80 = 40(N)
因為題目給的條件可知 `vec(R)` 是 3,4,5三角形,所以`vec(R)/5=40/4`
`vec(R)=50(N)`
A 196.4N
B 250N
C 306.4N
D 436.4N
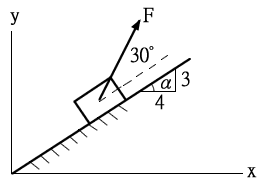

如圖所示,x 方向的分力
500×cos(30°+α)
500×cos30°cosα-sin30°sinα)
cosα=4/5=0.8,sinα=3/5=0.6
cos30°=`sqrt(3)/2`=0.866,sin30°=1/2=0.5
500×0.866×0.8-0.5×0.6)
500×(0.6928-0.3)
500×0.3928
=196.4(N)
A `50N`,↙
B ` 50N`,↗
C `50sqrt(3)N`,↙
D `50sqrt(3)N`,↗
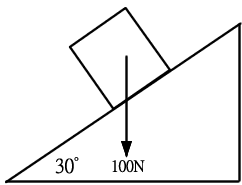

沿斜面的分力 = 100×sin30°
= 100×1/2
= 50(N)
A 20N
B 50N
C 70N
D 90N

如圖所示

`vec(F_3)`可以分解成 `vec(水平)` 跟 `vec(垂直)` 分量(紅色)
因為 `vec(F_3)` 是 5,12,13三角形
`vec(水平)` = 130*12/13 = 120N,垂直分量 = 130*5/13 = 50N
`vec(水平)` 跟`vec(F_1)` 分向相反,所以抵消,剩下120 – 80 = 40(N)
因為題目給的條件可知 `vec(R)` 是 3,4,5三角形,所以`vec(R_(垂直))/3=40/4`
`vec(R_(垂直))=30(N)`
50-F2=30
F2=20(N)
A 一個單力若無任何條件之限制,可以分解成無窮多個分力
B 一個單力若無任何條件之限制,可以分解成分力及力偶矩的組合
C 一個單力所分解出的各分力不必相互垂直
D 一個單力所分解出的各分力必小於該單力
一個單力所分解出的各分力不一定小於該單力
本網站提供的試題,僅供自我練習,並不保証完全正確。試題如有疏漏、錯誤,請E-mail告訴我們,我們會儘快更正。
時間在那裡! 成就就在那裡!
Once in a blue moon.(千載難逢)