Positive SSL
BLOCK
BLOCK
1 下列有關同平面力系之合力的敘述，何者正確？
A 兩個指向相同而大小不相等之平行力的合力位置，為在較大單力之外側
B 兩個指向相反而大小不相等之平行力的合力位置在二力之間，且靠近較大單力
C 兩個指向相反而大小不相等之平行力的合力位置在二力之間，且靠近較小單力
D 同平面兩個以上的平行力，其合力矩可能為0
  

兩個指向相同而大小不相等之平行力的合力位置，為在較大單力之外側內側

兩個指向相反而大小不相等之平行力的合力位置在二力之間外側，且靠近較大單力

二個指向相反而大小不相等之平行力的合力位置在二力之間外側，且靠近較小單力大單力

2 若有三個大小相等的同平面力，作用於同一點而達平衡，則可推知任二力間的夾角為
A 45°
B 60°
C 90°
D 120°
3 對於一組共xy平面不共點不平行的平衡力系，其正確的平衡方程式為
A ∑Fx = 0；∑MA = 0；∑MB = 0，其中A、B為xy平面上任意點
B ∑Fy = 0；∑MA = 0；∑MB = 0，其中A、B為xy平面上任意點
C ∑Fx = 0；∑Fy = 0；∑MA = 0，其中A為xy平面上任意點
D ∑MA = 0；∑MB = 0；∑MC = 0，其中A、B、C為xy平面上任意點
4 同平面不共點力系之合力（單力）之位置可依下列何種定理去求解？
A 虎克定律
B 瓦銳蘭定理(力矩定理)
C 拉密定理
D 波義耳定理
5 下列何者不屬於二力構件之平衡條件？
A 作用在同一點上
B 作用在同一直線上
C 大小相等
D 方向相反
6 如圖所示之三力呈平衡狀態，則
A F1＝12kN，F2＝7.2kN
B F1＝12kN，F2＝9.6kN
C F1＝20kN，F2＝16kN
D F1＝20kN，F2＝12kN
  

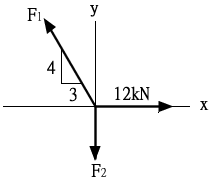
F1可以分成 －x 方向分力跟 y 方向分力

F1分成 －x 方向分力會跟12(kN)扺消

F1×3/5=12

F1=20(kN)

F1分成 y 方向分力會跟F2扺消

F2 = F1×4/5=20×4/5=16(kN)

7 如圖所示之共點力系，若處於平衡狀態，則 F2 之大小應為多少N？ 91
A 108
B 140
C 157
D 187
  

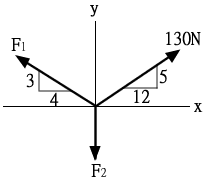
∑Fx=0

130×12/13－F1×4/5=0

F1=150N

∑Fy=0

150×3/5+130×5/13=F2

F2=140(N)

8 如圖所示，求此力系合力之大小與方向？
A 20N，37°
B 25N，53°
C 25N，127°
D 20N，53°
  

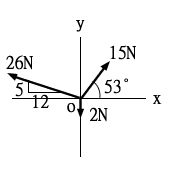
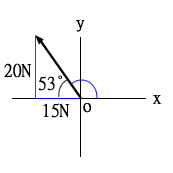
∑Fx=15×cos53°－26×12/13

=15×3/5－24

=15×3/5－24

－15N

∑Fy=15×sin53°+26×5/13－2

=15×4/5+10－2

=12+8

=20N

R=`sqrt((-15)^2+20^2)`

=25N

方向 = `tan^(-1)(20/(-15))`

用圖解:345的三角形，可知對20N那邊的角度是53°，所以方向就是180°-53°=127°

9 如圖所示，一共平面四個平行力作用於一橫樑上，試求此四力之合力R距A點之距離X為多少m？ 103
A 2m
B 3m
C 4m
D 5m
  

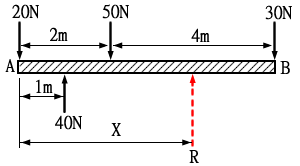
合力R=∑Fy

=20+50+30-40=60(N，↓)

∑MA=20×0+50×2+30×6－40×1

=100+180－40=240(N．m，順時針)

∑MA=60．X=240

X=4(m)

合力R的方向是向下與圖示相反，圖示R只是假設的方向

10 如圖所示，試求四力之合力距A點之距離為若干?
A 3m
B 4m
C 5m
D 6m
  

合力R=∑Fy

=20+30+10－15=45(N，↓)

∑MA=20×0+30×4+10×9－15×2

=120+90－30=180(N．m，順時針)

∑MA=45．X=180

X=4(m)