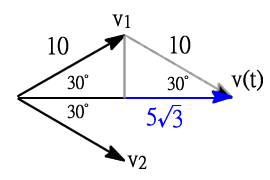
30° 60° 90°三角形比例`1:sqrt(3):2`,由圖可知,v(t)角度 0°,大小 `5sqrt(3)*2` =`10sqrt(3)` = 17.3V; `v(t)= 17.3sin(377t)(V)`
交直流混合波是一交流波形含有直流成份
直流成份的直流值 VDC = 3
交流波形的有效值 Vrms = `(-4sqrt(2))/sqrt(2)`
混合波有效值 = `sqrt((V_(DC))^2+(Vrms)^2)` = `sqrt(3^2+((-4sqrt(2))/sqrt(2))^2)`
=`sqrt(9+16)` = 5
交直流混合波是一交流波形含有直流成份
直流成份的直流值 VDC = `-3`
交流波形的有效值 Vrms = `(4sqrt(2))/sqrt(2)`
交直流混合波的有效值 = `sqrt((V_(DC))^2+(Vrms)^2)`= `sqrt(3^2+((4sqrt(2))/sqrt(2))^2)`
= `sqrt(9+16)` = 5
交直流混合波的直流值 = 直流值 VDC = `-3V`
`-3/5 = - 0.6 `
A 頻率50Hz、B 頻率`50/(2π)=7.95Hz`
算功率要用有效值(不是平均值)
`V_(A(rms))=sqrt(5^2*64/100)= 4V`
`P_A=4^2/100=0.16W`
`V_(B(rms))=5/sqrt(2)=3.53V`
`P_B=(5/sqrt(2))^2/50=0.25W`
`V_(A(DC))=5*0.64=3.2V`
`V_(B(DC))=5*0.636=3.18V`
正弦波瞬時電壓表示式: `v(t)=V_msin(ωt)`
`V_(rms)=110V ;V_m = 110sqrt(2)V`
`f=60Hz`; `ω = 2πf` `= 2*60*π` `= 120π`
`V_(t)=110sqrt(2) sin(120πt)`
sinθ最大值=1
v(t) 最大值 = `v(t)= 4sqrt(2) + 6 =11.656V`
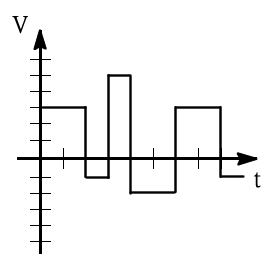
`V_(DC)` = `(3*2+(-1)*1+5*1+(-2)*2)/6` = `1V`
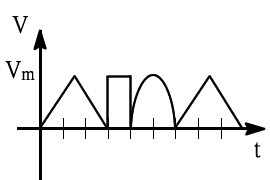
有效值 = 均方根值
先平方 再 平均 再 開平方根
波形平方並不好算,可以用有效值反推回去,觀念如下:
`有效值= sqrt((波形平方和)/(週期T)`
`有效值^2 = (波形平方和)/T`
`有效值^2xxT = 波形平方和`
該波形有效值算法如下:`V_(rms)` = `sqrt((((10)/(sqrt3))^2*3+10^2*1+((10)/(sqrt2))^2*2)/6)`
= `sqrt(50)` = `5sqrt2(V)`

三角波 FF = 1.155
正弦波 FF = 1.11
方波 FF = 1
餘弦波 FF = 正弦波 FF = 1.11